●統計の難しさ
統計がなぜ難しいのか、それは言葉と式が難しいから
統計はマジックであり、ふさわしい解析方法を選ぶことが重要である
どんなデータにどんな解析がいいのか、それを知ることが先決

数学的には正しいことが医学的に正しいとは限らない
統計は実学であり、もっともよく当てはまる統計モデルを使用する。
統計を行うときはリンゴを切るときに似ており、2つに切るところを5,6個に切ってみて、虫食い(あたり)を見つけることができた。そこまでやることが大事。
試行錯誤して悩むことが大事、データをよく観察し自分の中でresearch questionを持ちながら 隠された「答え」を発見してほしい。

●答えの発見方法
研究を行うとき仮説を持つが、まずphase-1として検証を行い仮説をもとに解析をしていき有意さが出れば、正解。
しかし現実には不正解が出ることが多い。不正解が出たときにphase2で何が言えるのか、というclinical questionを元に考え、自分が調整していない因子があるのではないか、何か足りない群分けがあるのはないか、新規因子で入れなきゃいけないものが抜けているのではないか、と文献検索をしたりする。
すると、新発見が必ず出てきて、それを元に論文化できるのではないかと考えている。なんども解析をするしかない。

●どっちのFried Potatoがお得？(平均とSD)
A君とB君がマックでポテトを買った。どちらが欲しいか。
実際は損得はないように見えるが、バラツキがあるかどうかを見る。
バラツキがあるなしを見て、バラツキがない方が、良いように見える。

●バラツキの指標：分散と標準偏差SD
それはバラツキを見てほしい。A君のポテトはバラツキがないのに対してB君のポテトはバラツキがある。選ぶのであればA君のポテト。
分散と標準偏差は統計ソフト持っていなくともどちらもExcelで行うことができる。

●標準偏差はバラツキの指標
平均とSDを求めていく。今回は２群間の比較を行う。
パラメトリックとノンパラメトリック。
パラメトリックは100回ボールを投げたときに正規分布しているかしていないかということ
まず自分がデータを入手した時にはそれが正規分布するかそうでないかを考える。
もし正規分布しているデータであれば、平均値プラスエラーバーを書いていく。
正規分布していない場合、ノンパラメトリックの場合は中央値、ただのバー、分散を書いて表に表していく。どちらを使えばいいか。

●正規分布に従うかどうか
自分のnが少なく、バラツキが大きければ正規分布しない。
nが多ければ、バラツキが少なく正規分布しやすい
正規分布していない方が有意差が出にくい
自分がわからないときはノンパラメトリックを選択する
もしノンパラで有意差が出たということなら確実に出ているということ
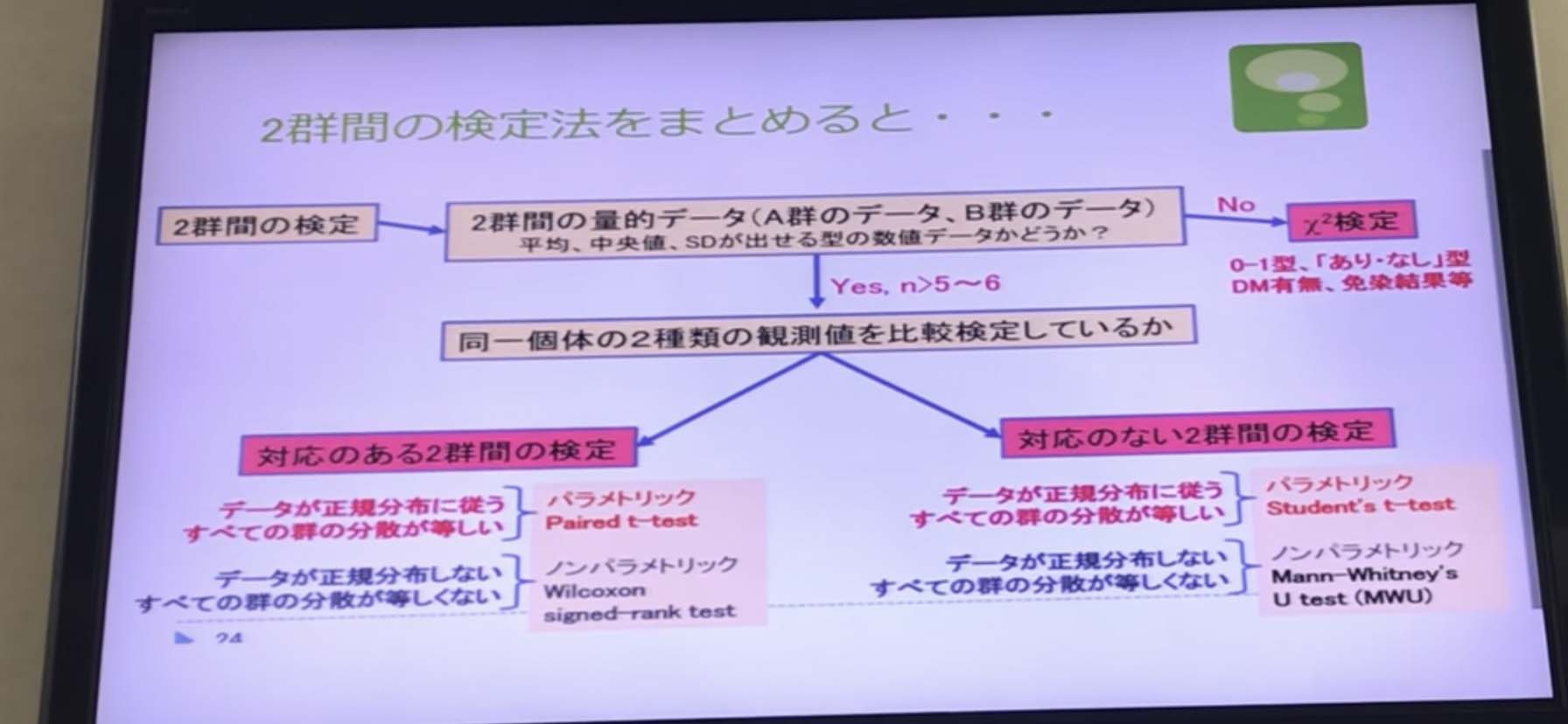
対応のある、なしは同一個体の２種類の観測値を比較検定しているかどうか、とうこと。していれば対応があることになる。

●対応のない２群の比較検定
独立した２群のデータに有意差があるか？(棒や点グラフが適切)

Parametric:Student t –test:スチューデントのt 検定
平均値を比較して検定する。Excel関数で計測可能。平均値とSDの棒グラフで表記する。nが多く、ばらつき(2群の分散が一緒)が均一なとき使える
Non-parametric : Mann-Whitney’s U test:マン・ホイットニ検定
中央値を比較して検定する
Excel マクロで計算可能。中央値と分布図の点グラフで表記する。nが少なく、
ばらつき(2群の分散が一緒)が異なるときに使う。正規分布の適合性が少ないときはこちらで計算を行う。

●対応のある２群の比較検定
同一個体に、ある刺激による変化(=差)に有意差があるか(折れ線グラフが適切)
・Parametric : Paired t- test :対応のあるt検定
・Non-parametric : Wilcoxonsigned-rank test:ウィルコクサン符号付順位検定
この４つを覚えるとよい。

●３群間の検定
・対応のない３群間の検定
パラメトリック：One way ANOVA
ノンパラメトリック：Kruskal-Wallis test
・対応のある３群間の検定
パラメトリック：One way repeated measures ANOVA
ノンパラメトリック：Friedman test

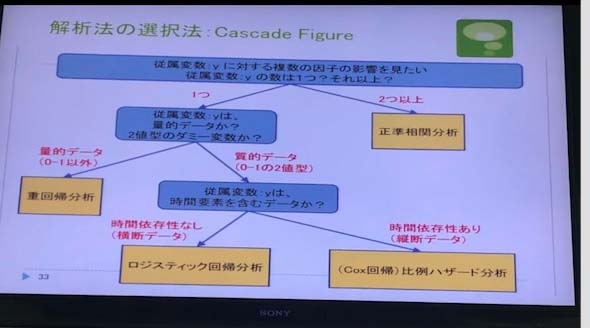
●多変量解析について

多変量解析の用語：従属変数y、独立変数x、はしっかりと

cox回帰比例ハザード分析
ロジスティック回帰分析：従属変数が1-0の場合
重回帰分析：連続の場合

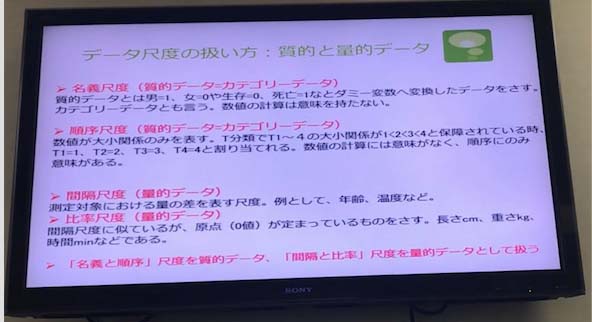
●データ尺度の扱いかた、質的と量的データ

●解析法の選択法
1-0で見ているか見ていないか

●単変量と多変量の使い分け
P valueに関わらず性別と年齢は入れていただきたい

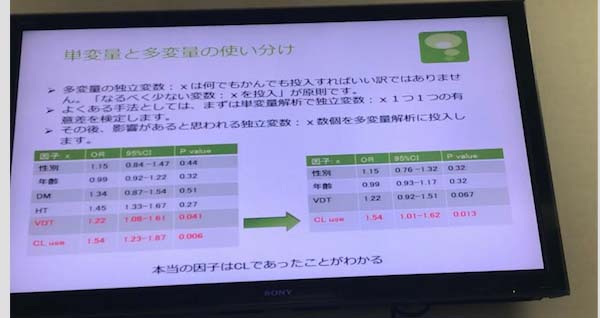
●ではどうやって独立変数を選ぶのか？
たくさん入れてしまうと解析ができなくなり意味がわからなくなる
探索研究の場合には何も出ないことが十分にありうる

●独立変数の選択：症例数の問題


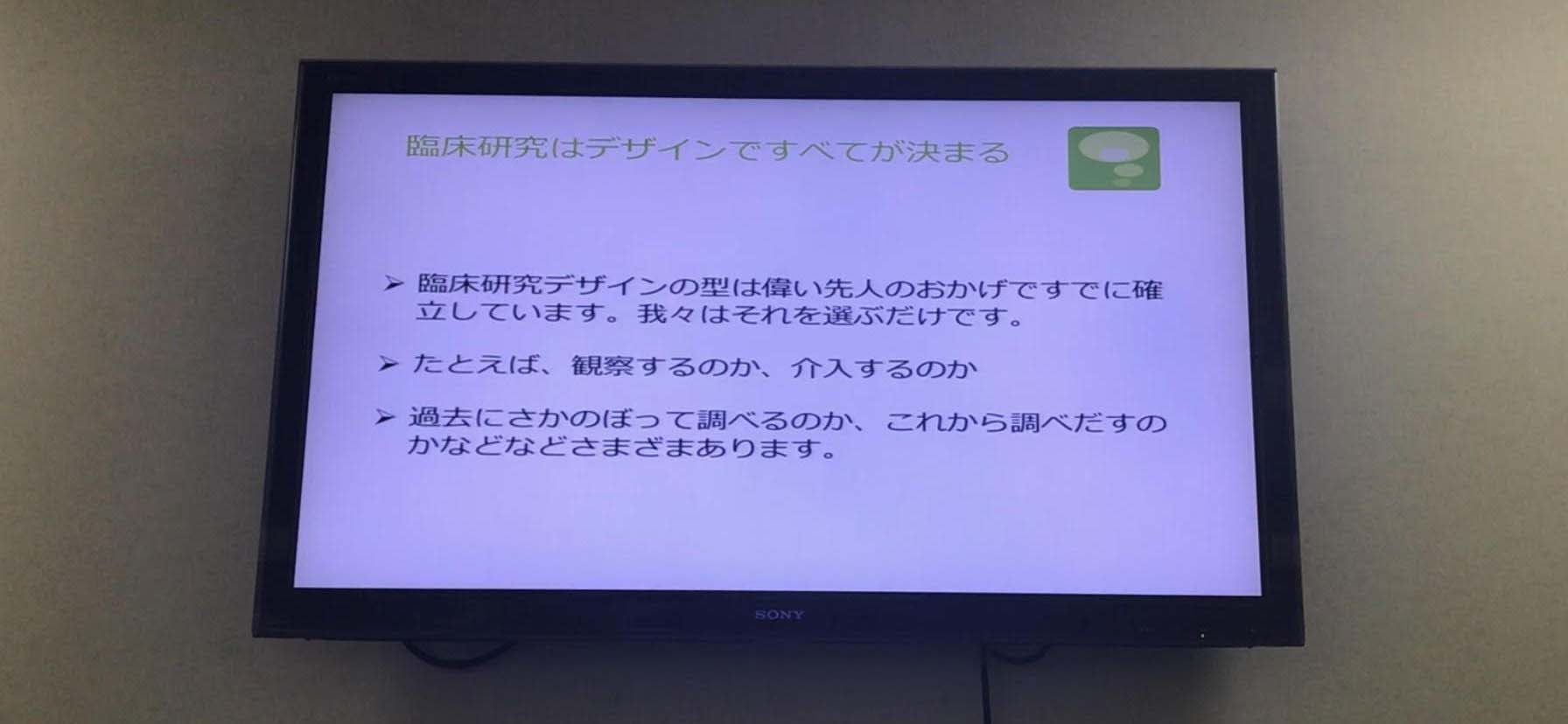
●観察研究と介入研究

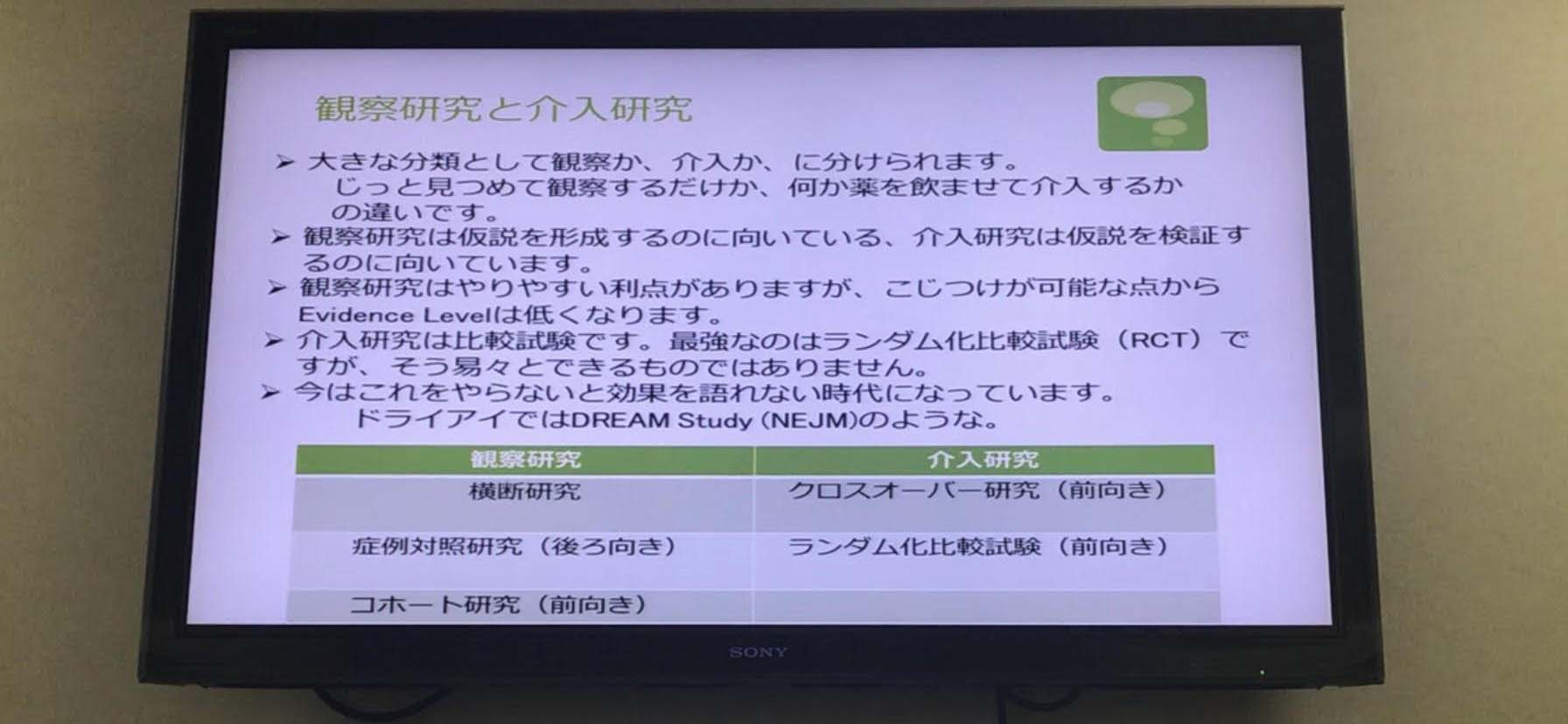
●横断研究のエッセンス
安く簡単にできる

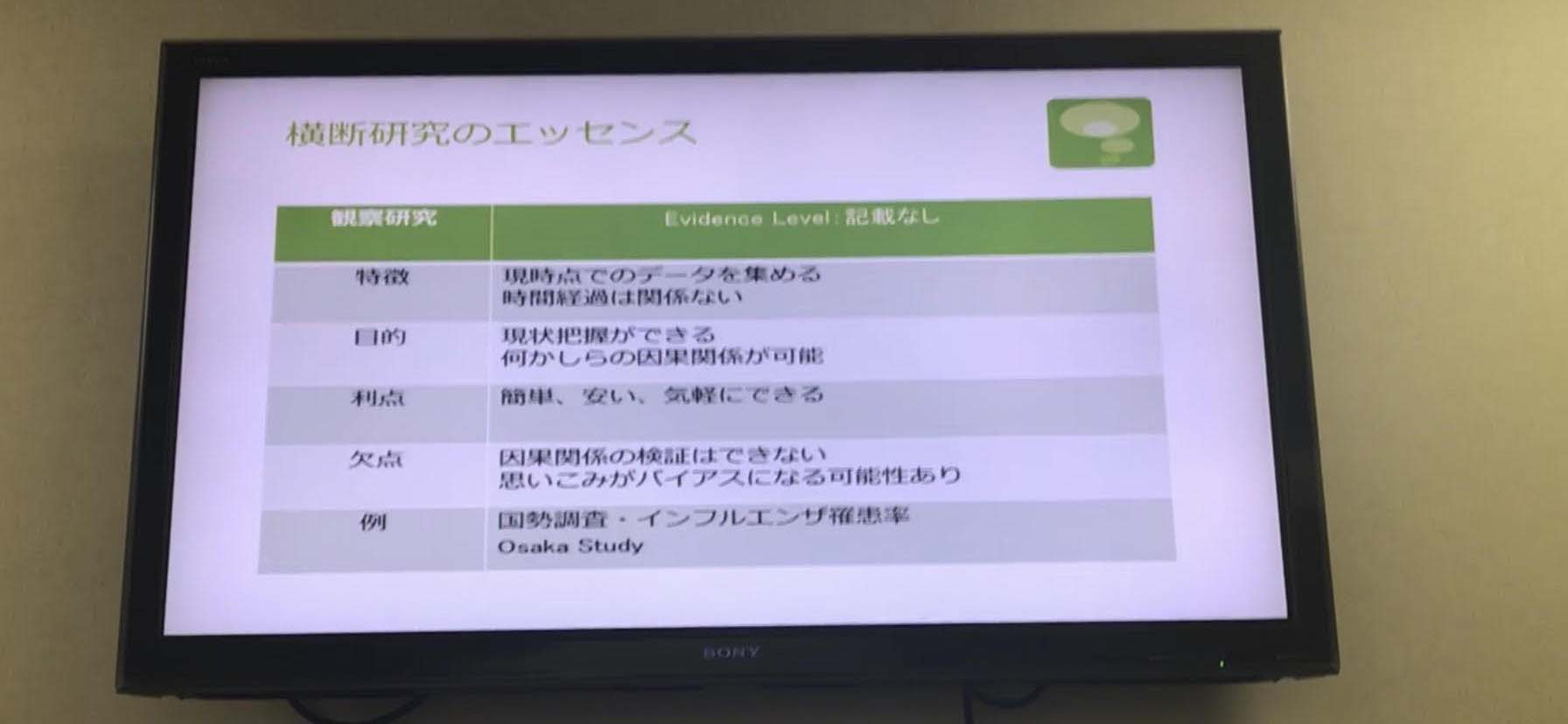
●ケースコントロールスタディ研究のエッセンス


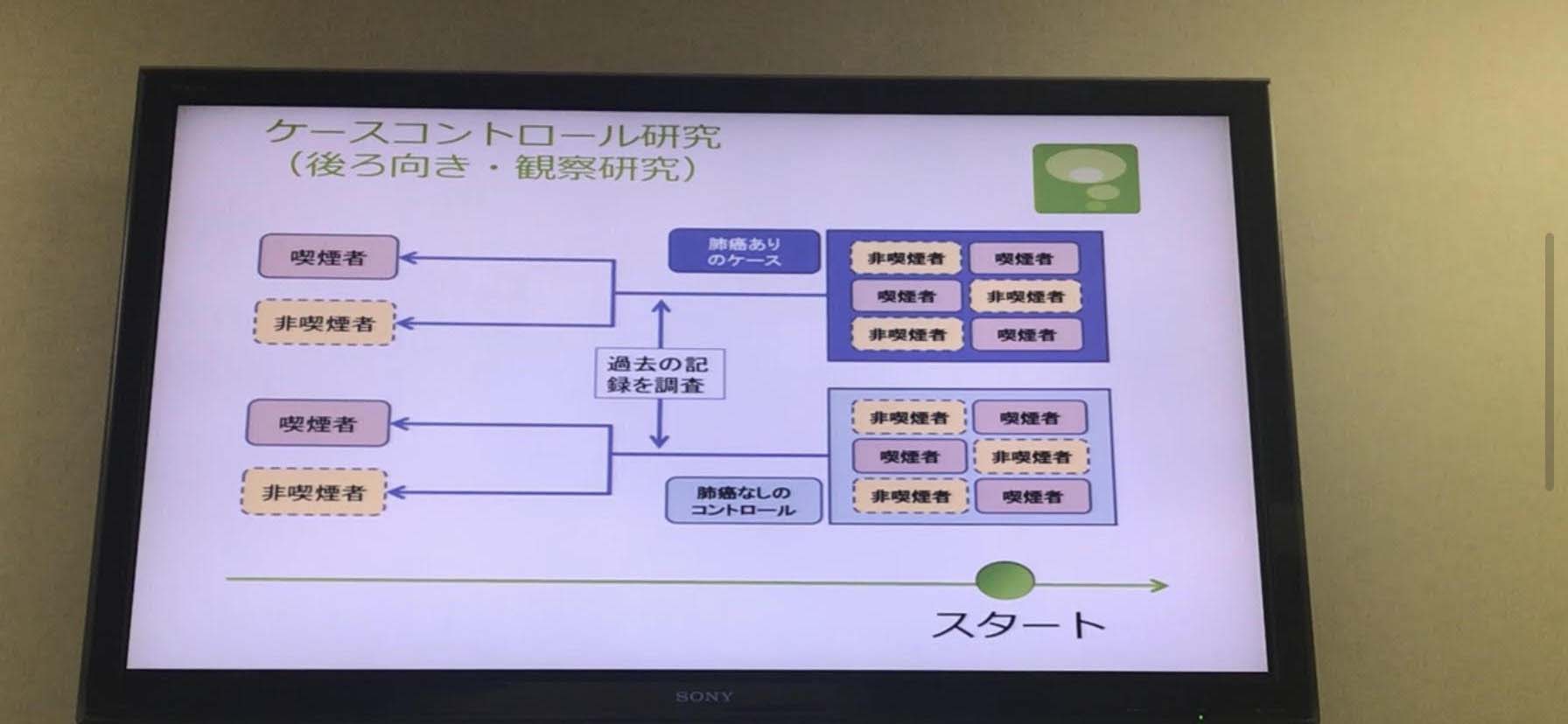
●コホート研究前向、観察研究
時間軸が決定している

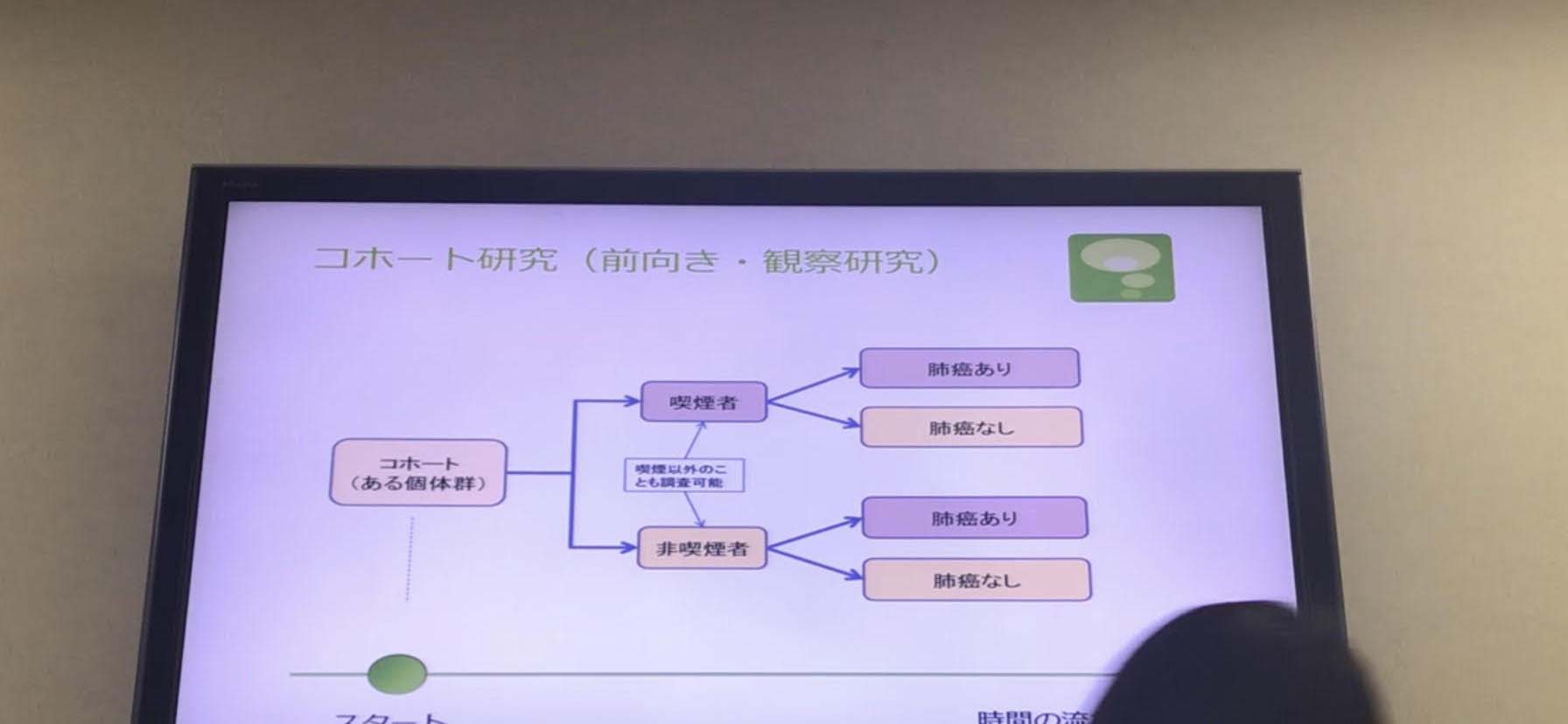
●コホート研究のエッセンス
時間とお金がすごくかかる、筑西検診もそれ　調査のしつも保ちにくい

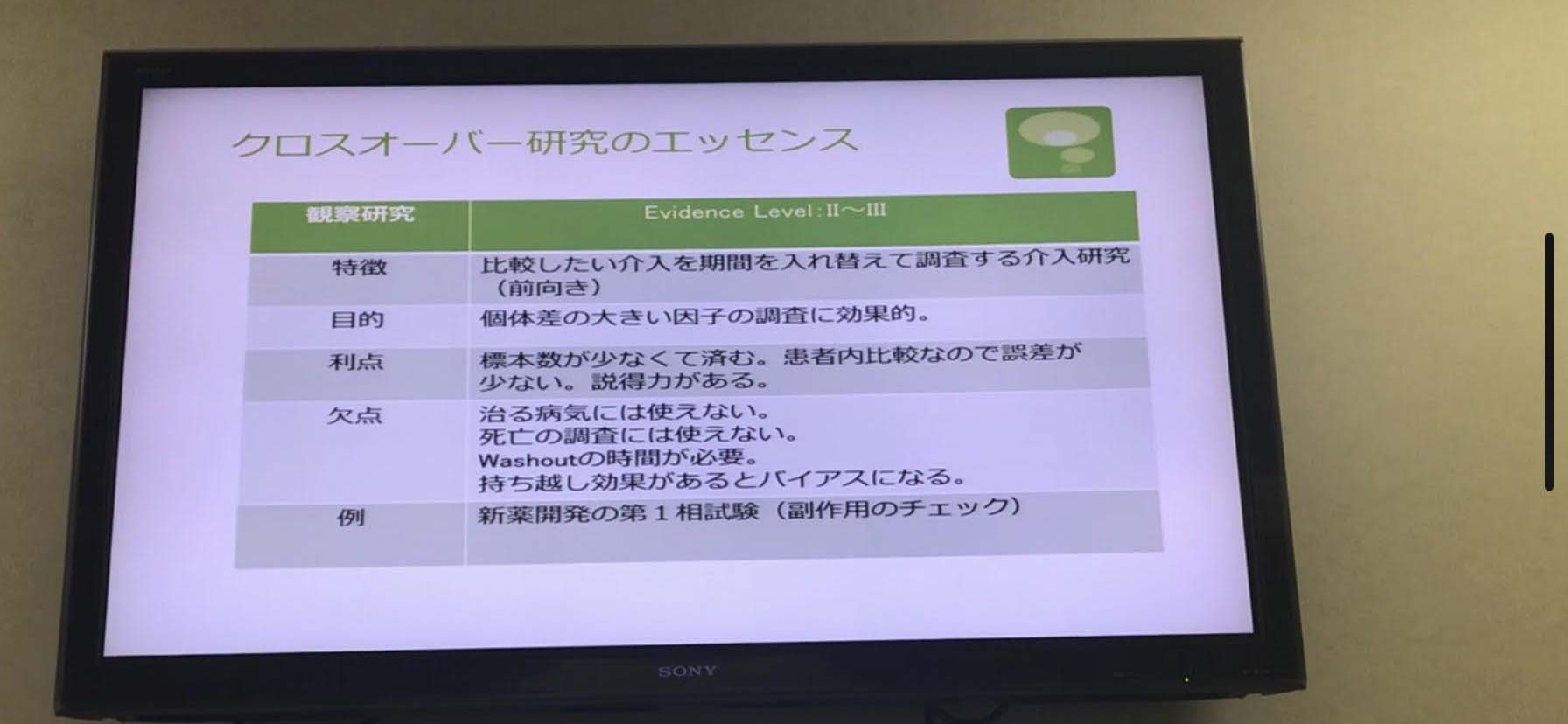
●クロスオーバー研究(前向き、介入研究)
新薬作成の際に行われる。Wash-out期間が出てきてしまうが、標本数が少なくてもできる。患者間での比較なので誤差が少ない。

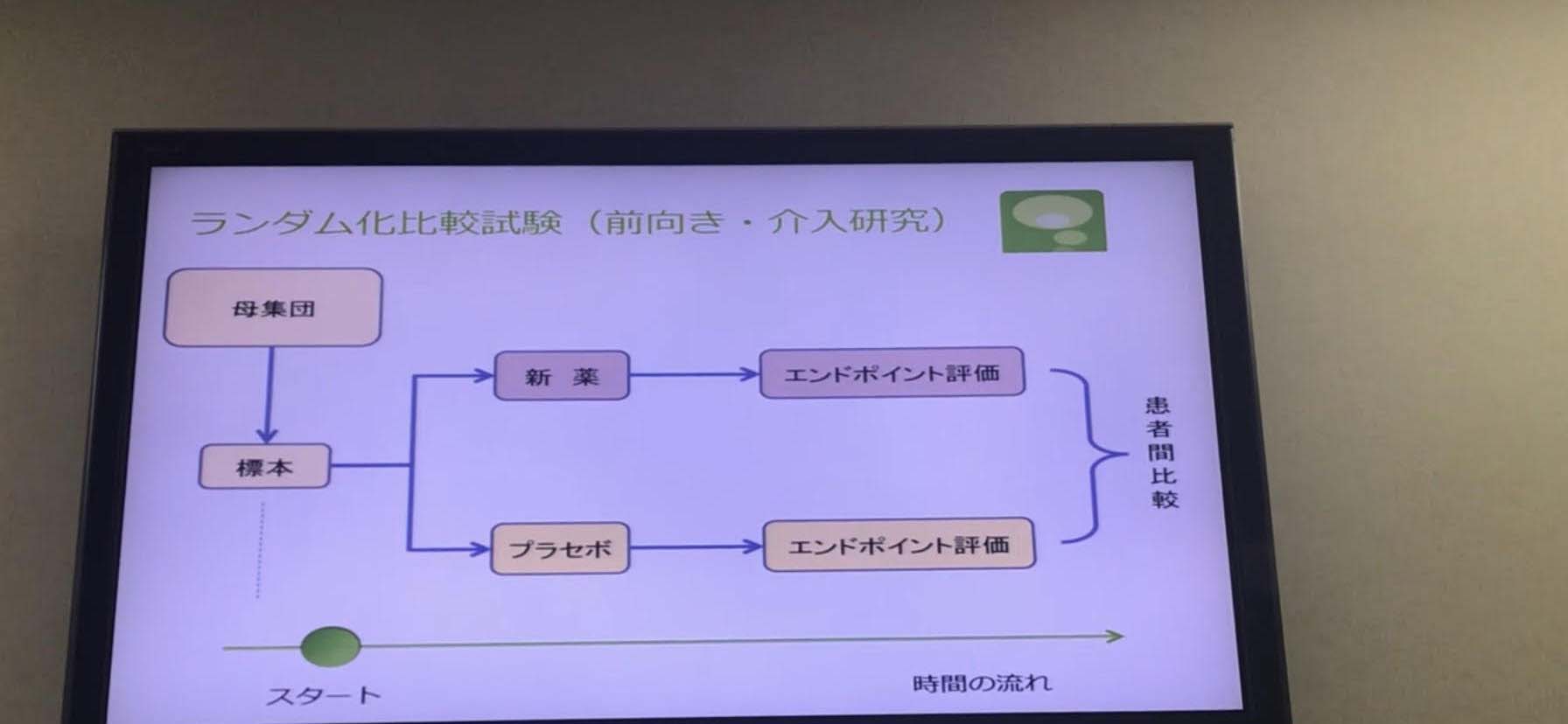
●ランダム化比較試験

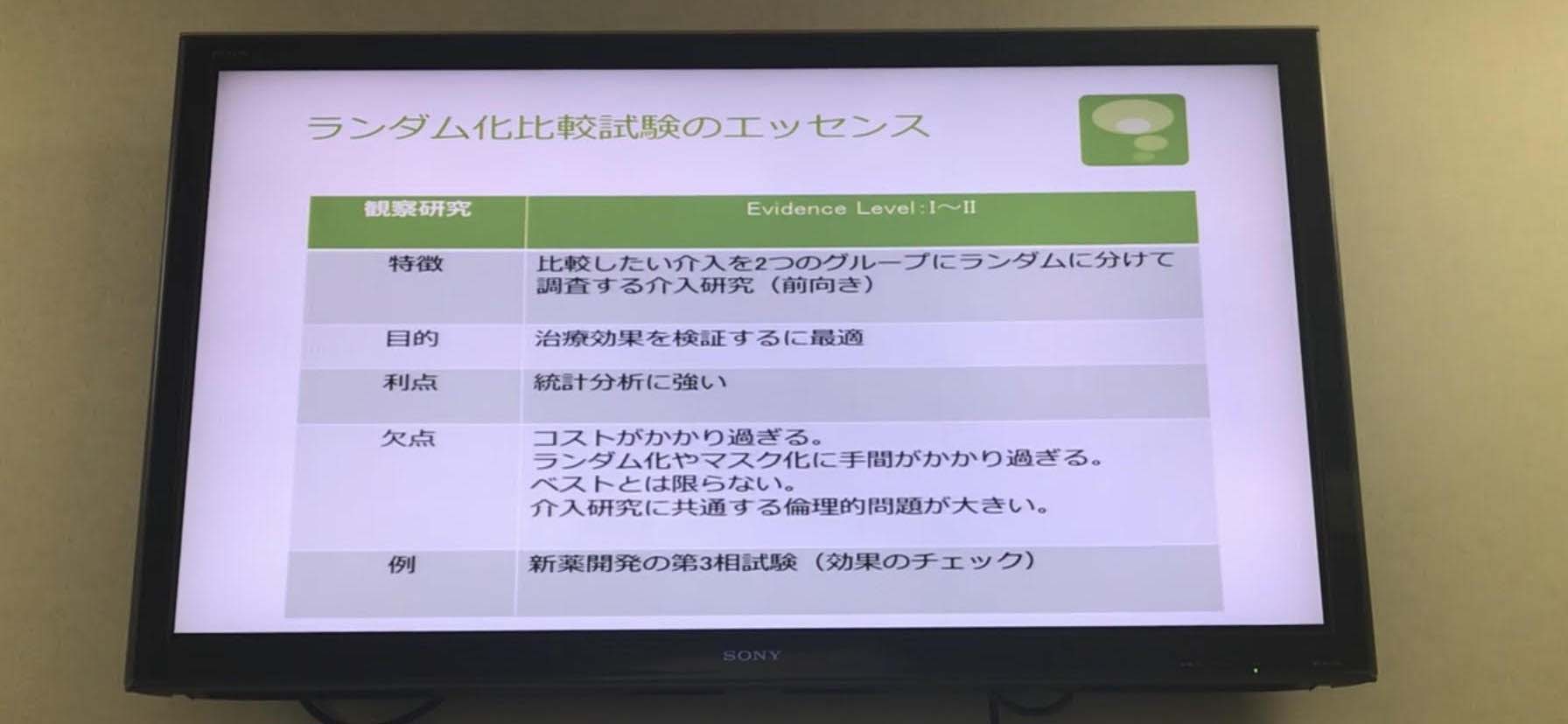
●ランダム化比較試験のエッセンス
コストがかかる、第三相試験のチェックによく使われる

●DAG；Directed Acyclic Graph
交絡因子は最後に解析をするときにはadjustをいなければならない

●検診と糖尿病罹患率
交絡因子となるものはあるか→？にあたる部分に【健康への意識が高い】がはいる。どれくらい高いか入れなければならない。

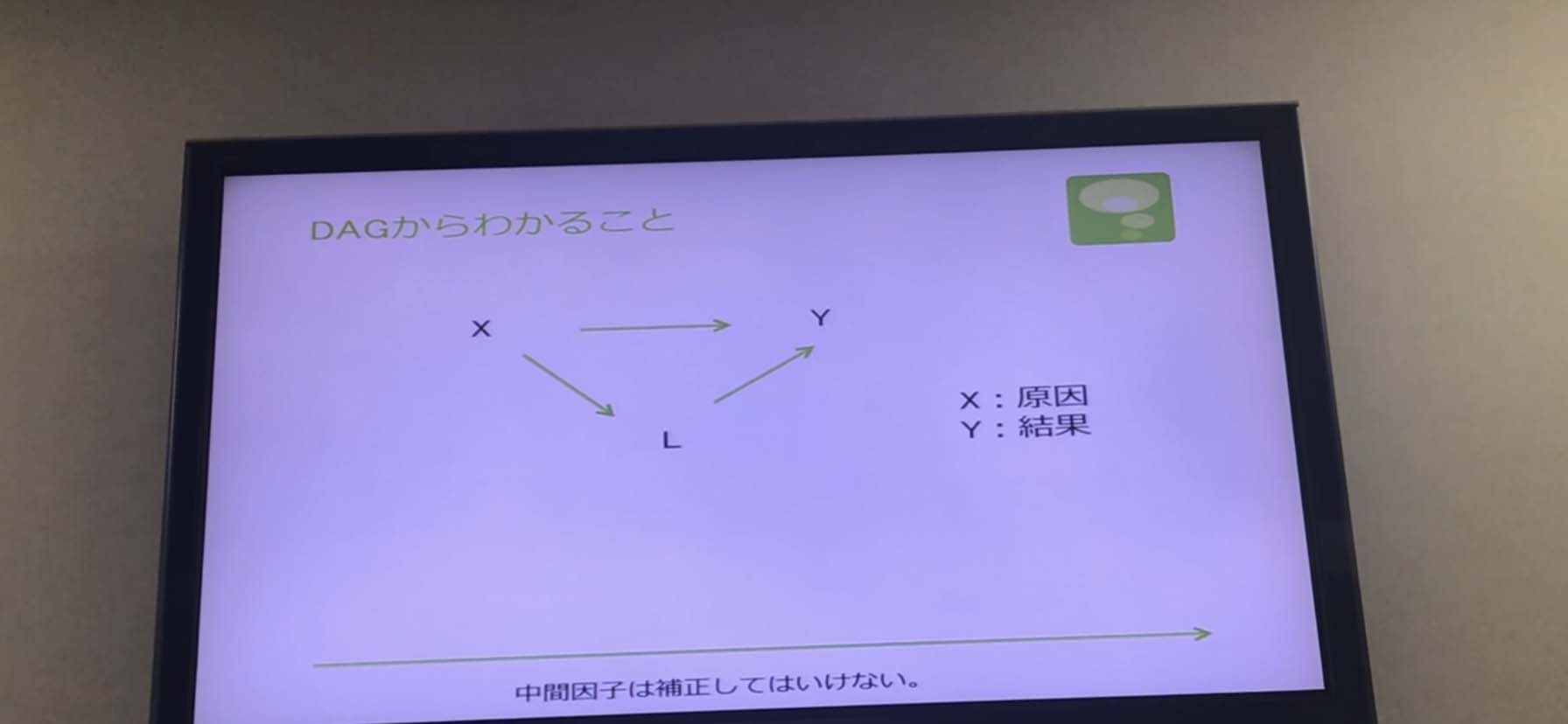
●DAGからわかること
仮に運動していない人を除去したとしても、中間因子は補正してはいけない

●5本ノック
上から○○○×○

●終わりに
解析をしていて一回でも解析して諦めない
何度でも解析し直しても宝物を見つけてください
ご静聴ありがとうございました。